CS 421
Problem Set 6
Greedy Algorithms and Basic Graph Algorithms
(25 points)
"I want an Oompa-Loompa!' screamed Veruca."
-- Roald Dahl, Charlie and the Chocolate Factory
Readings
This problem set covers material covered in Chapters 16 and 22 of the textbook.
Notes
Mark the top sheet with your name and the names of any students with whom you collaborated. If you didn't collaborate with anyone, mark your collaborators as "None."
Begin each problem at the top of a sheet of paper, front or back. That means for three problems you should turn in at least two sheets of paper: front and back of the first one, and front of the second. That's at a minimum; there is no maximum. And be sure to staple your pages together. Homework not following these guidelines will be returned and marked down for being late.
Remember, your goal is to communicate. Full credit will be given only to correct solutions which are described clearly. Convoluted and obtuse descriptions will receive low marks. Show ALL of your work.
To complete your homework, you may ONLY consult the following material:
Problems
Problem 1 (5 pts). Making Change
The change-making problem involves giving change for a specific amount n with the least number of coins of demonimations d1 > d2 > ... > dm. In the U.S., the most widely used coin denominations are d1 = 25, d2 = 10, d3 = 5 and d4 = 1.
Problem 2 (10 pts). Huffman Coding
Problem 3 (10 pts). Depth-First Search and Breadth-First Search
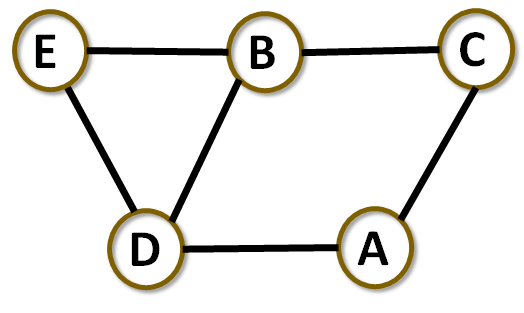
Extra Credit (5 pts)
Decision Tree.
Design a strategy that minimizes the expected number of questions asked in the following game:
You have a deck of cards that consists of one ace of spades, two deuces of spades, three threes, and so on up to nine nines, for a total of 45 cards in all. Someone draws a card from the shuffled deck, which you have to identify by asking questions answerable with a 'yes' or a 'no'.